Behind The Numbers: Attack Modifiers Explained
In this article we’ll explain how to calculate an Operator’s Final Attack stat after attack modifiers have been applied. To avoid confusion of terms, we will refer to it as Final_ATK. The formulas presented here are not of my creation. They were shared with me by Kawa and come from the RIHQ Discord. My goal is to share them in a concise format, explain what they mean, and list Operators that have relevant abilities. I am not a mathematical genius, in fact numbers frighten me, so if you find any errors in my calculations or conclusions, please contact me via Discord.
- Note: For a broader view of the entire DPS calculation, see our reference guide:
There are two different types of buffs that can increase an Operators Attack: Attack buffs and Attack multipliers. Both of these affect the Final_ATK of an Operator, though in different fundamental ways. We will present the details of how each contributes to the calculation.
- Note: This is NOT the damage formula. Final_ATK is used as part of the damage formula.
We’ll start by defining a few terms that will be used in our calculation later.
Base_Attack
Base_Attack is the Attack stat of the Operator. It can be seen in-game under Operator Attributes under ATK.
- Note: The in-game displayed value already includes any ATK gained from Trust.
We can see Amiya’s Base_Attack at E1 Level 45 with Trust at 98% highlighted in the following image:
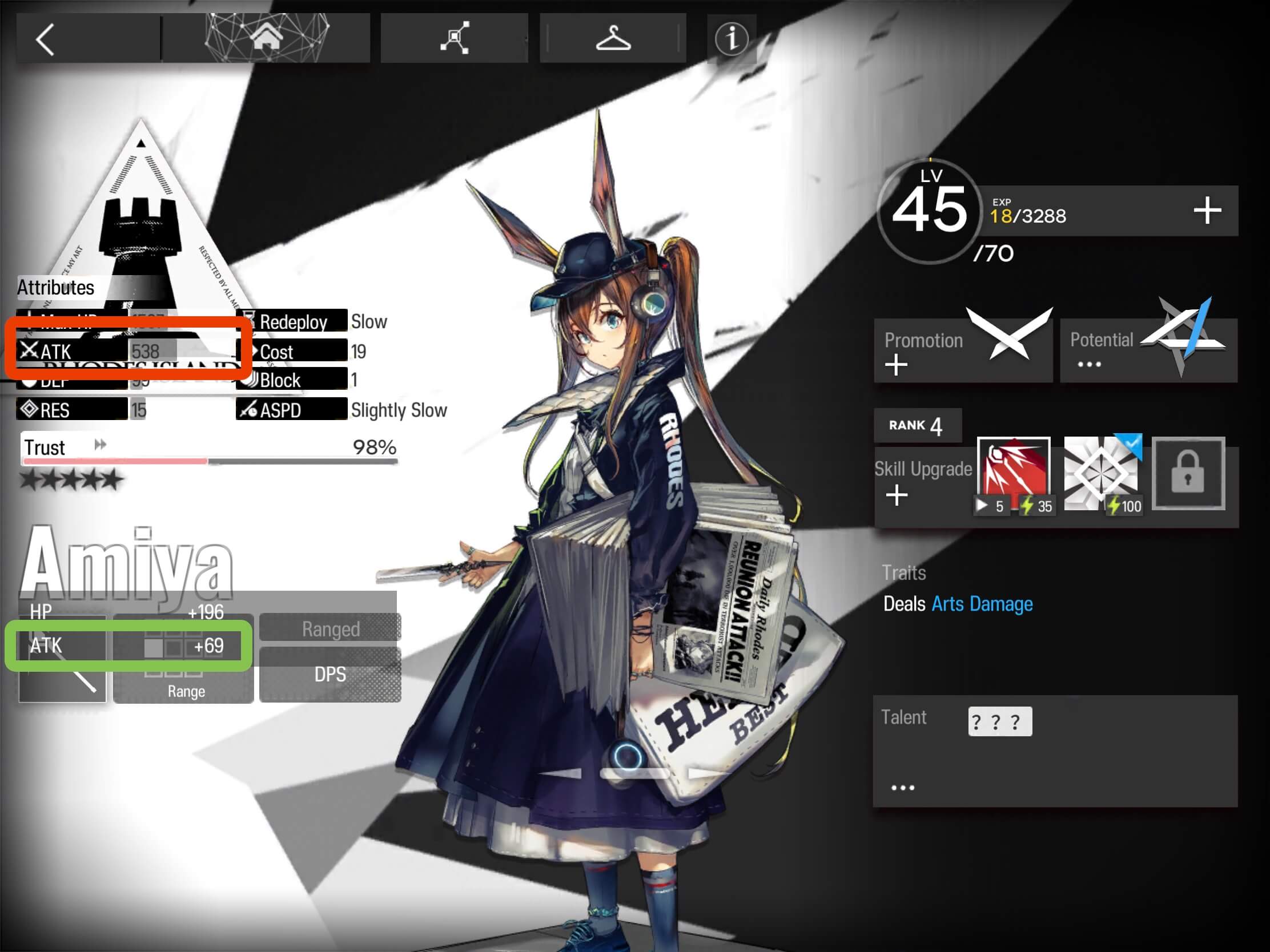
The Base_ATK is shown in the red box as 538. This already has the ATK gained from her Trust level, 69, shown in the green box.
Base_ATK_Buff
Base_ATK_Buff is the summation of all ATK percentage increases applied to the Operator by Talents or Skills. Base_ATK_Buff is applied as a percentage increase to Base_Attack, and buffs are identified by a + in front of the ATK number.
Here is an example of Base_ATK_Buff applied by Franka’s Skills:
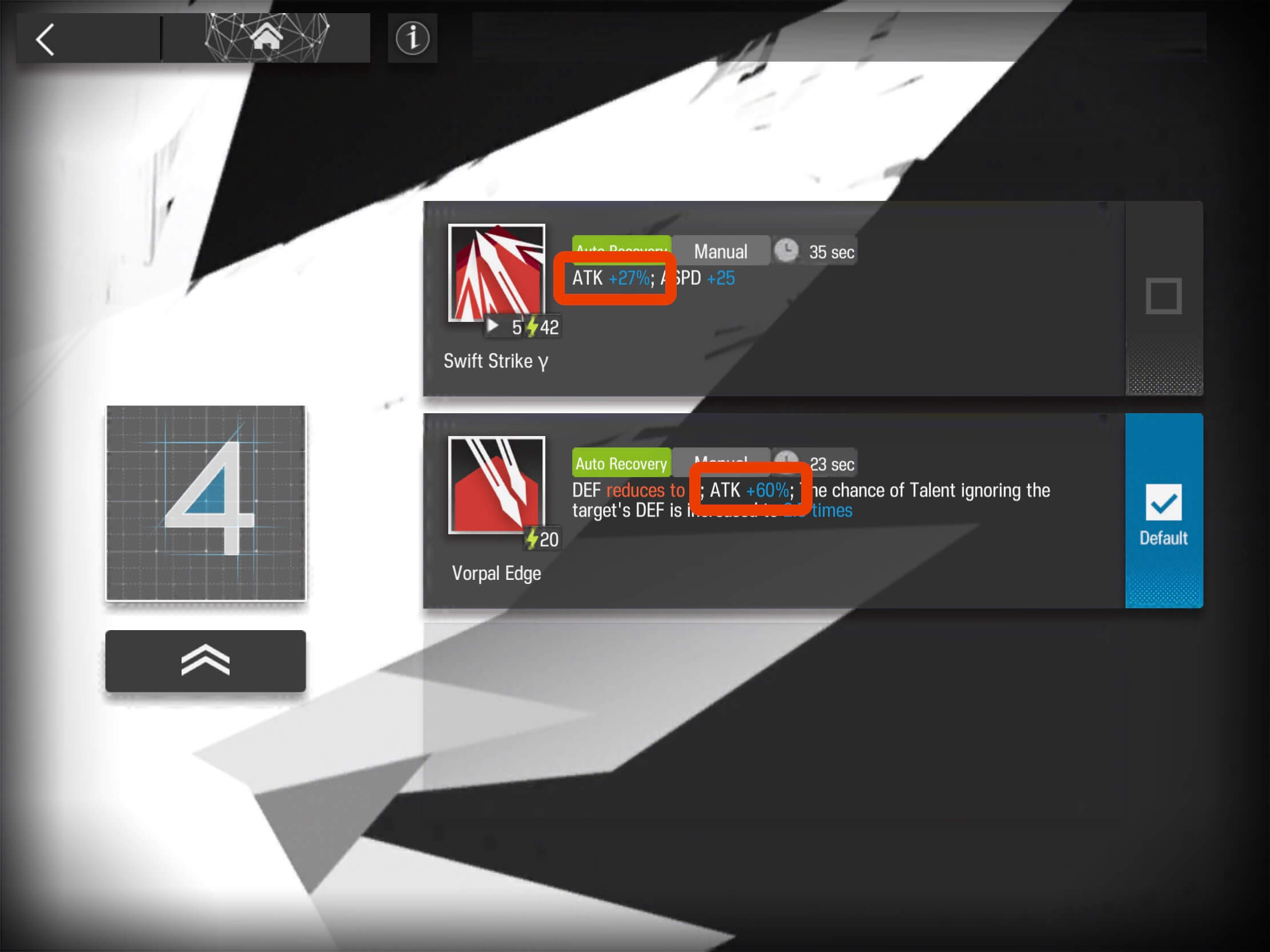
Thus, in the above example, Franka’s Skill 1 increases her Base_Attack by 27%, where her Skill 2 increases it by 60%.
- Note: One exception is Provence’s Skill 1 Wolf’s Eye. It isn’t clear exactly how this buff is applied, though the basic idea is: The less HP the enemy has, the higher her ATK, roughly scaled at X% per 20% HP, where X is defined by Skill description.
-
Sora - Skill 2 - Hymn of Battle
-
Note: Sora’s Skill 2 has a unique application in the Final_Attack formula that will be discussed in the next Section.
-
-
Zima - Skill 2 - Ursus’s Roar
-
Castle-3 - Talent - Tactical Configuration 1
-
Dobermann - Talent - Starter Instructor
-
Gavial - Talent - Battlefield Medic
-
Exusiai - Talent - Angel’s Blessing
-
Siege - Talent - King of Beasts
-
Eyjafjalla - Talent - Pyrobreath
-
Skadi - Talent - Abyssal Predator
-
Warfarin - Skill - Unstable Plasma
-
Swire - Talent - Melee Combat Guidance
Sora_SK2_Buff
Supporter Operator Sora’s Skill 2, Hymn of Battle, has a unique role in the formula for Final_ATK. It adds a flat amount of ATK to the Base_ATK_Buffed Base_ATK based on a percentage of her own Attack (this will be shown in more detail in a later formula). The formula for how much ATK Sora adds is:
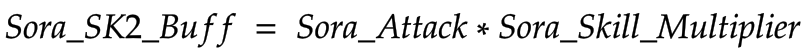
Sora_Skill_Multiplier can be found on the Skill page and is determined by Skill Level, as shown here:

From this we can see that at Skill Level 4 Sora_Skill_Multiplier = 80%. Sora_Attack at E1 Level 40 and Trust 100% = 298. In that case, our Sora_SK2_Buff would be: 298 * 80% = 238.
Attack_Multiplier_Buff
The ATK_Multiplier_Buff is the ATK percentage value associated with any Talents or Skills that say things like “Increases ATK to X%” or “ X% of ATK” (identified by the absence of the + in front of the number). This number indicates a direct percentage that we will apply to the ATK value we previously derived from applying the Base_ATK_Buff and Sora_SK2_Buff to the Base_Attack. If there are multiple ATK_Multiplier_Buffs, they are all multiplicative.Thus, the formula is:
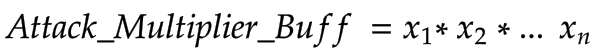
Where x is an ATK_Multiplier_Buff, and n is the number of buffs applied.
Here is an example of an ATK_Multiplier_Buff Savage’s Skill 1, Power Strike 𝝱 :
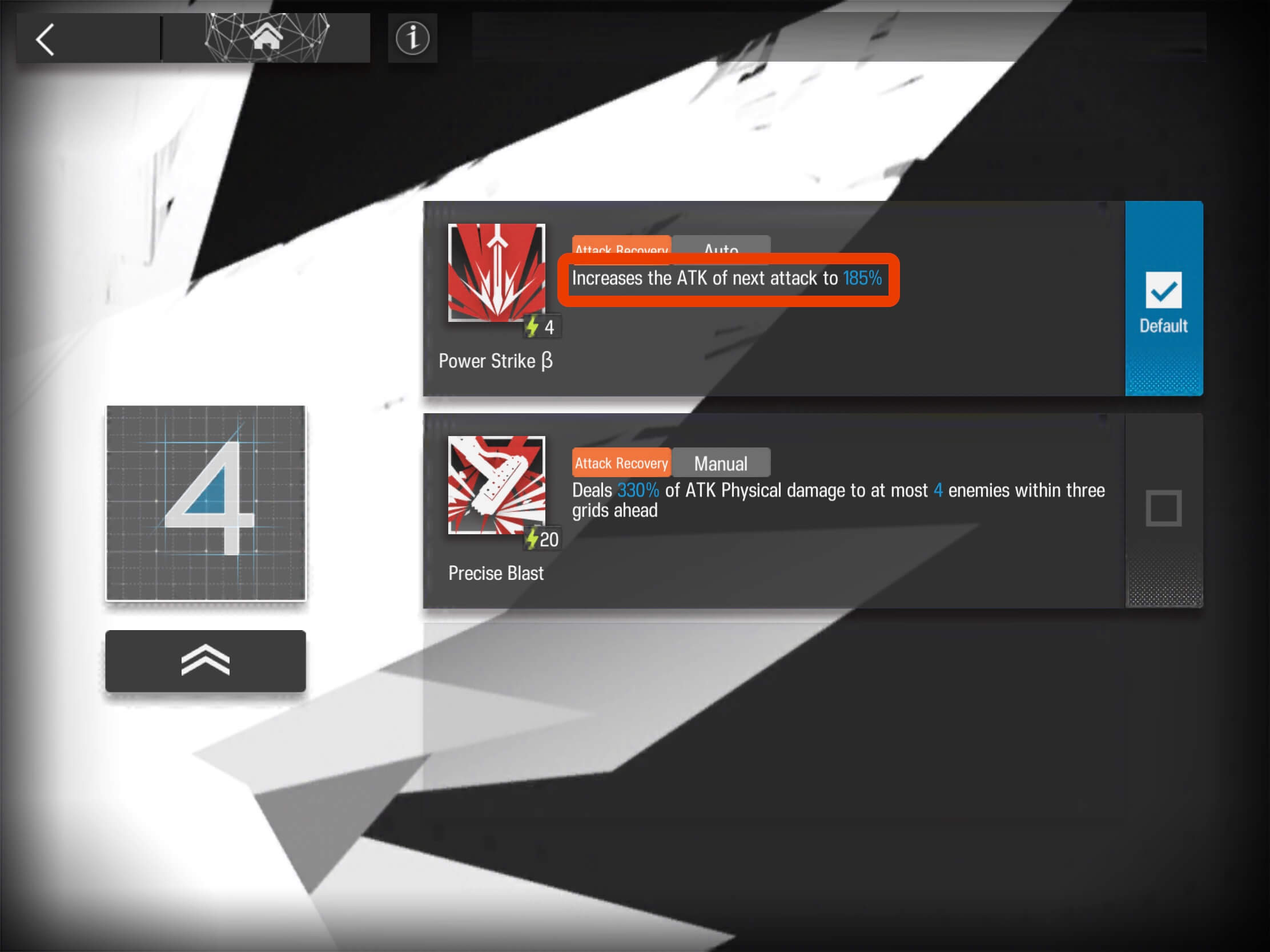
In this case, the Attack_Multiplier_Buff = 185%, representing an 85% increase in attack.
Final_ATK
We now have all the information we need to determine the Final_ATK of an Operator after all modifiers are applied.
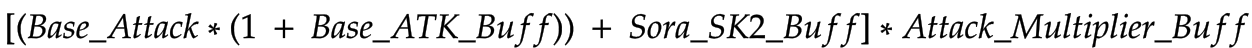
So what does this mean in English though?
-
First, apply any Base ATK buffs (ATK % with a +) to the Operators Base Attack.
-
Second, add the ATK from Sora’s Skill 2 if it applies.
-
Last, apply the ATK multiplier buff (ATK % without a +).
Major Takeaways
-
Same-type Base ATK buffs are additive with each other, where ATK multiplier buffs are multiplicative with each other and Base ATK buffs. This means, all else equal, additional ATK Multiplier buffs will provide better overall performance than additional Base ATK buffs because of the nature of diminishing relative gain of additive buffs.
-
Sora’s Skill 2 is additive with base ATK buffs, but multiplicative with ATK multiplier buffs. Thus, in general, she will be more effective at improving the latter.
Short Theoretical Example
Savage Base Attack = 500
Base Attack Buffs = 50%
Sora’s SK2 buff = 200
Attack Multiplier Buff = 150%
Final_ATK = [(500 * (1 + 50%)) + 200] * 150% = 1425
Realistic Example
Ok, that is a lot of math. Let’s run through an example to see how this works in practice. Let’s look at Savage at E1 Level 40 Potential 1 and 75% Trust while using her Skill 1, Power Strike 𝝱, at Skill Level 4 and assuming she has the ATK buff from Castle-3’s Talent Tactical Configuration 1 at level 1 Potential 1. Also, that she has the buff from Sora’s Skill 2 Hymn of Battle, and for simplicity sake, we’ll say the buff provides 298 ATK under the conditions calculated in the Section above. Also her Talent Valley is active. No other ATK modifiers are present.
First we’ll find Savage’s Base_Attack. Looking here we can see it is 474.
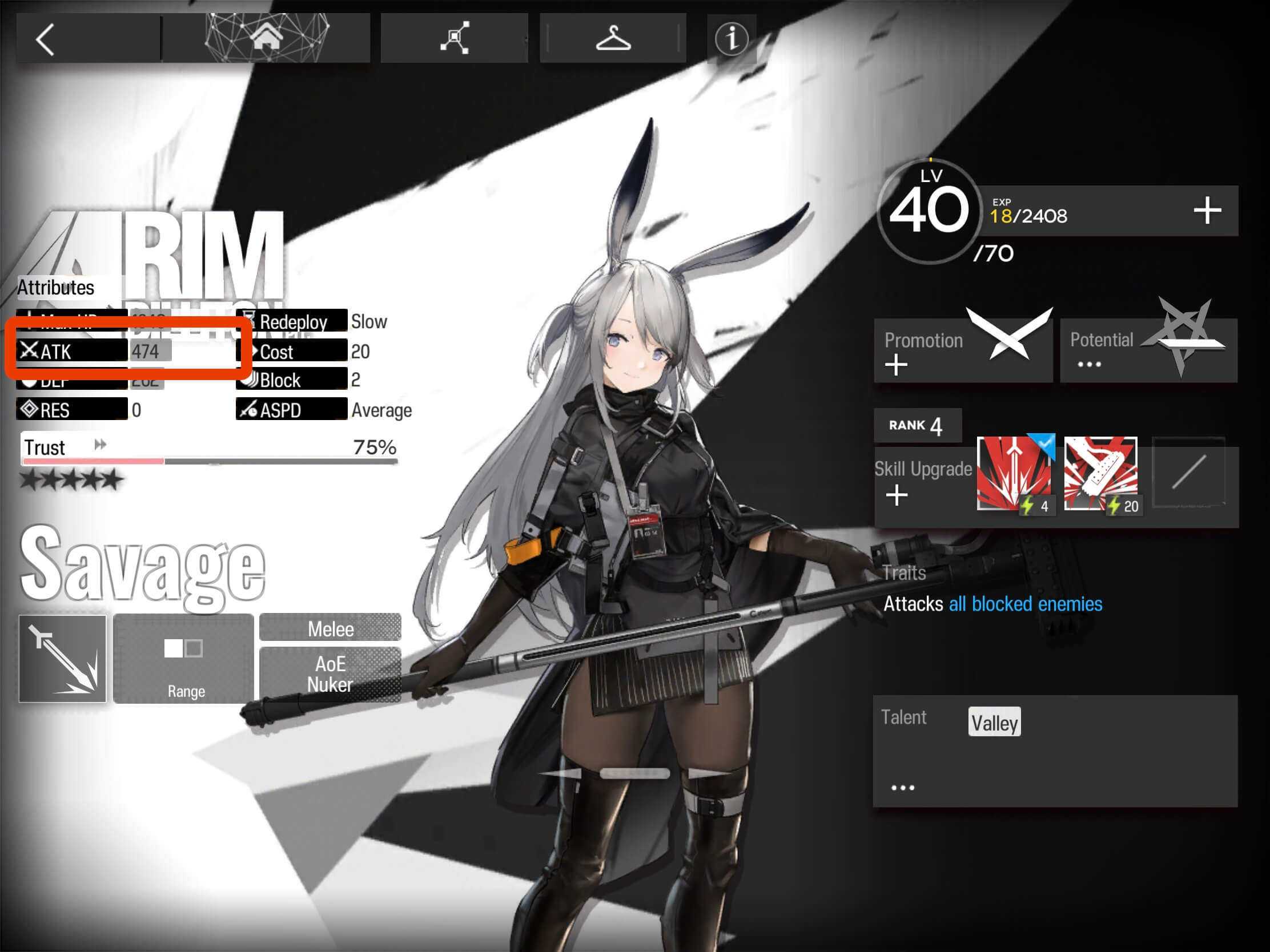
Next we’ll find the Base_ATK_Buffs. From Castle-3’s Talent, we get 10%, as seen here:
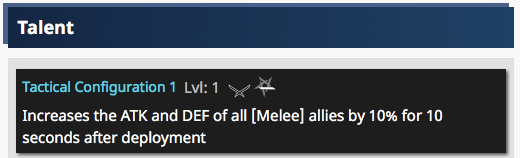
From Savage’s Talent we get another 5%.
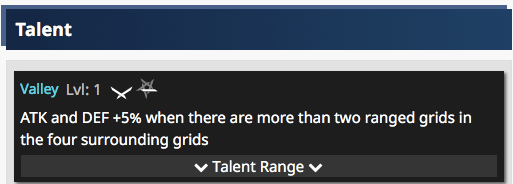
Thus, our total ATK_Buffs = 10 + 5 = 15%.
Sora_SK2_Buff = 298, as stated above.
Last, we have our Attack_Multipler_Buffs = 185%, as seen here:
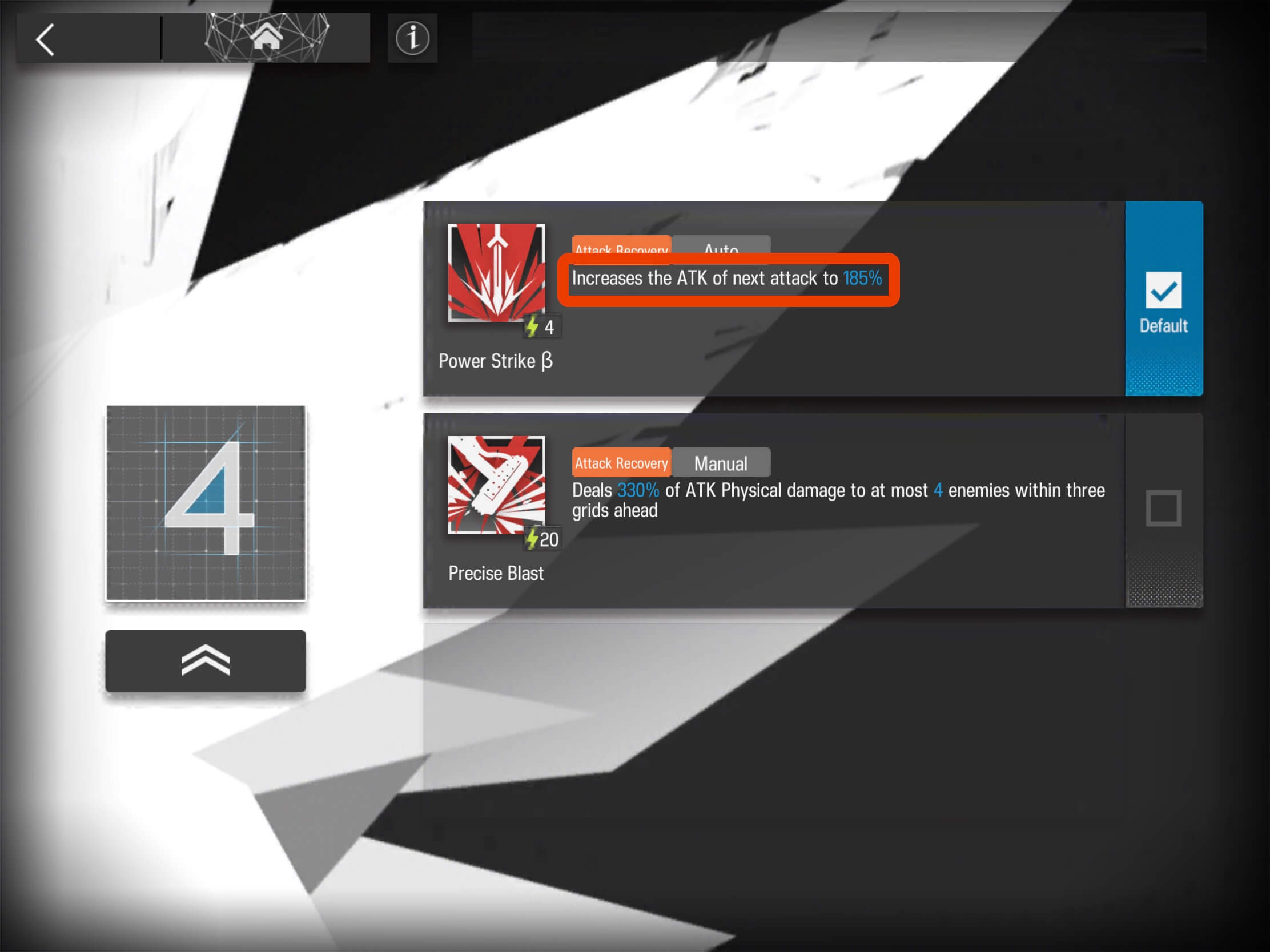
We now have the information to calculate Final_Attack as follows:
Final_ATK = [(474 * (1 + 15%)) + 298] * 185% = 1,560











